Detailed analysis of the microwave background radiation gives practically our only direct evidence of conditions before galaxy formation. The spectral shape and departures from perfect isotropies give (temporal and angular) evidence on the existence of structures at the epoch of recombination, which is the last view we currently have until galaxies and AGN begin to take shape at some epoch like z=10 (or whatever it is...). Two very useful references for much of the material in these final lectures are Peacock's Cosmological Physics (Cambridge 1999) and Galaxy Formation by Longair (Springer 1998). The existence of a recombination epoch happens because the densities of matter and radiation have different dependences on the cosmic scale factor (1/R³ versus 1/R4).
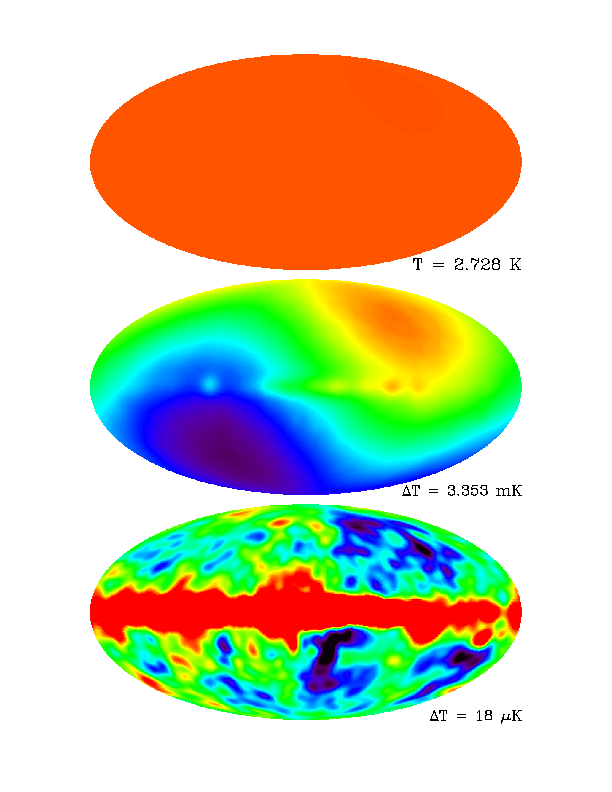
The best-known maps of fluctuations in the background are from the COBE Differential Microwave Radiometer (DMR). These images illustrate the four-year data products as measured at 53 GHz, in galactic coordinates with the galactic center in the middle. At the top is the overall background temperature (blank to an excellent approximation), then in the middle we see the result at a magnified stretch with the mean value removed. This shows the dipole interpreted as a Doppler shift due to motion of the Milky Way with respect to the sphere of matter now seen radiating in the background, and some of the residual contamination from the Galactic foreground. Finally at the bottom we see the all-sky fluctuations with the dipole removed (note, by the way, that we cannot separate any intrinsic dipole structure in the CMBR from effects of our relative motion). The individual fluctuations at high galactic latitudes are now significant (which was an improvement over the initial announcements based on 2-year maps from the data). The Tenerife and South Pole experiments also confirmed individual structures. A further advance and unification of structures on various scales came with the first maps from the Wilkinson Microwave Anisotropy Probe (WMAP), shown below the COBE results.

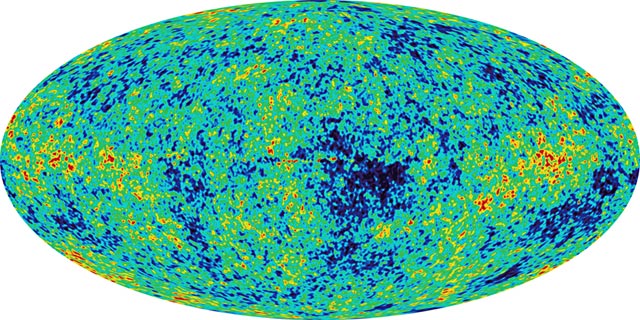
There are several distinct origins for fluctuations in the CMBR, telling us about various properties of the baryonic Universe and important on various scales. Straight density fluctuations will control just when a given volume element recombines through the n² dependence of recombination rate. Density inhomogeneities will translate to temperature fluctuations, since denser regions have shorter recombination times and thus decouple earlier (at higher redshift and thus appearing dimmer = colder). In these so-called adiabatic fluctuations, the temperature amplitude we see is 1/3 the density amplitude (which traces back to photon density varying as T³). A competing effect, which turns out to be negligible on small scales compared to density fluctuations but probably dominant on larger scales, is the Sachs-Wolfe effect, basically the gravitational redshift on photons escaping from denser regions. The fluctuation amplitude depends on the potential Φ: &delta T/T = δ Φ >/3c². In addition, velocity structure can introduce Doppler fluctuations in observed temperature, of magnitude δT/T = δ v . r / c. The fluctuation amplitudes are always very small, so that linear perturbation theory can be used.
The horizon size at the last-scattering surface, important not only for big questions of causal connectivity but in the growth of perturbations, is 184 (Ω h²) -1/2 Mpc. The spectrum of fluctuations (usually considered as a power spectrum in wavenember l of, for example, Bessel functions on the sphere) is highly diagnostic of processes in the early Universe, which has driven much of the work on improving maps of structure in the CMBR. We expect a Sachs-Wolfe "plateau" for small values of l, leading to an acoustic (or Doppler) peak. The location of this peak is sensitive to both Ω and Λ, while its amplitude is sensitive almost purely to Ω. Models also predict that harmonics of this peak should be seen to higher values of l. These may be explored with the publicly released CMBFAST code (see Seljak and Zaldarriaga 1996 ApJ 469, 437, more recently updated to include both closed and open geometries, with the interesting difference that only spatially wrapped spherical wavenumbers are allowed in the closed case). This typical prediction was taken from the MAP WWW site, which includes further versions showing the effects of varying cosmological parameters:
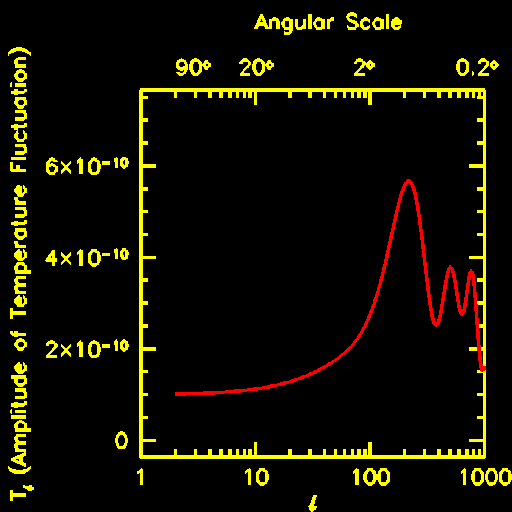
The really new aspect of the WMAP results is in covering a wide range of angualar scales at high sgnal-to-noise ratio in a single experiment, dramatically reducing the potential role of systematic errors. (In fact, for low values of l, one becvomes limited now by cosmic variance - the fact that we have only one slice of the early Universer to observe, and we must work with whatever it happens to present). In deriving cosmological quantities, one usually niormalizes the power to what we see locally (say on 100-Mpc scales). The total density parameter Ω tot shifts the location of the first (strongest) peak to smaller l for higher values; this is a curvature measurement giving the relative scales between then and now. The baryon density by itself changes the peak ratios of odd and even peaks (through dissipation in compressive phases of the acoustic motions). Large values of the cosmological constant Λ move the first peak to higher l and lower amplitude, while both baryon density and H0 affect the height of the peaks. A helpful way to see why such effects happen is to note that the Universe at recombination was pervaded by a field of velocity perturbations transmitted acoustically (now that was different). We see this field slices with the redshift width of the time it took to complete recombination, so smaller-scale fluctuations will be damped out. The peaks and valleys tell what scales had the right timing to constructively or destructively interfere, since for a given wavnumber k the phase follows ei s k t where s is the sound speed.
While brief, the epoch of recombination did have a nonzero duration, which translates into a finite thickness in redshift. As set out by Jones and Wyse (1985 A&A 149, 144), the cosmological dependences cancel almost perfectly giving an optical-depth function τ(z) = 0.37 (z/1000)14.25. Thus the distribution of last-scattering redshift (specifically e-τ dτ/dz) is strongly peaked, almost Gaussian with mean of z=1065 and standard deviation σz = 80. (WMAP data give zrec = 1089 ± 97). This will modify the spectrum slightly with respect to a perfect single-temperature blackbody, and will be manifested by damping out irregularities due to structure which is smaller than the comoving depth of this apparent shell. Details of the recombination process have been recently re-examined by Seager, Sasselov, and Scott (2000, ApJS 128, 431) using full radiative transfer codes and sophisticated models for all the relevant ions, who found that Peebles (1968 ApJ 153, 1) and Zel'dovich et al. (1968 JETP Lett. 28, 146) did remarkably well in reducing the problem to approximate differental equations. Further details exist, but at about the level of uncertainty in some of the relevant reaction rates. In evaluating the spectrum of the background radiation, it is noteworthy (see the treatment by Peacock, for example) that the thermal form of the radiation spectrum was established when brehmsstrahlung was active at redshift of order 106 and no major additional input between then and recombination is allowed by the existing limits on departures from a Planck form.
Further developments should come fast, with NASA's Wilkinson Microwave Anisotropy Probe (WMAP) still operating in the L2 region and and ESA's Planck in the pipeline. These should yield significant measurements of high-order harmonics in the fluctuation spectrum sufficient to measure the basic cosmological parameters by themselves.
Last changes: 11/2009 © 2000-9