Recombination lines (especially Hα): Line emission is characteristic of H II regions, zones of ionized gas around young star clusters that still contain OB stars (spectral types B0.5 and hotter). These stars are special in that they are hot enough to produce significant fluxes of ionizing radiation, shortward of the Lyman limit. H II regions may be found wholesale by narrow-band imaging at Hα if internal extinction is not too large, and also by radio surveys for recombination-line emission (though this works best in our own galaxy). To turn measures of emission-line intensity into star-formation rate, first consider the physics of photoionization and recombination. I use the notation from Osterbrock in Astrophysics of Gaseous Nebulae and Active Galactic Nuclei, which will be no great surprise to anyone looking at my graduate institution.
Hydrogen is ionized by absorption of Lyman continuum photons (λ « 912 Å, energy above 13.6 eV). The line radiation we detect arises from recombination of the electrons so released with another proton, and a cascade toward the ground state. This occurs with a recombination rate α, such that
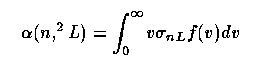
in terms of the electron velocity distribution f(v) and cross-section for capture to quantum state n,2L given by σ{nL. We deal only with the state 2L since cascades to here occur very rapidly. The velocity distribution may be taken as a thermal (Maxwellian) form in the electron temperature T (in fact defining this temperature):
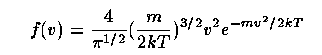
because, even though the electrons are released with a different f(v), Coulomb interactions with ions (predominantly protons) thermalize their velocities on a timescale short compared to the recombination time. In the so-called nebular approximation, the atom is undisturbed after recombination, so that the subsequent radiative cascade is governed only by the radiative decay coefficients (Einstein A values); that is, the cascade is rapid compared to the photoionization timescale. Then the total capture coefficient (to all quantum states) is αA = Σn αn and the recombination time is
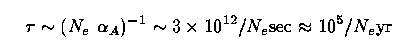
for Ne in cm-3. At high Lyman α optical depth (in most H II regions, for example), the cascade stops at n=2 due to resonant scattering of Lyman α line photons, so we also define a "case B" recombination coefficient, starting the sum above at n=2.
In equilibrium, there will be a balance between photoionization and recombination rates, which allows us to measure the ionizing UV luminosity of a star solely from the intensity of line radiation from surrounding ionized gas. In the ionization-bounded case, all of a star's ionizing flux is absorbed within the nebula (as opposed to matter-bounded, where all the material is ionized but some ionizing radiation escapes). Then the total number of Lyman-continuum photons produced by the star is
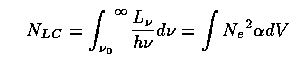
for electron density Ne (see Osterbrock's Astrophysics of Gaseous Nebulae and Active Galactic Nuclei for the gory details).
If we are dealing with a single star, the theory of stellar atmospheres predicts NLC as a function of spectral type (or effective temperature) and luminosity class (or evolutionary stage). Blackbodies are not necessarily good approximations to stellar spectra in this range. A conversion to rate of star formation schematically uses the luminosity (actually for this application the Lyman-continuum photon emission rate), lifetime, and mass, with a properly weighted average to account for the mix of stellar masses which contribute. As a benchmark, the number of O7 stars needed to produce a given Hβ luminosity is N(O7) = 3.4 x 10-37 L(Hβ) erg/sec. Hα is about 2.9 times as strong as Hβ under low-density conditions. Following Kennicutt 1983 (ApJ 272, 54) we may extrapolate using a representative initial-mass function (IMF) to the total star-formation rate above 10 solar masses: SFR = L(Hα) / 7.0 x 1041 erg/sec, in solar masses per year, and to a total SFR SFR = L(Hα / 1.12 x 1041 erg/sec. Different assumptions about the initial mass function will change these constants (especially a different lower-mass cutoff or slope on the lower main sequence). Recombination lines are sometimes spoken of as photon counters for these purposes.
Measurements of optical recombination lines (again, Hα is strongest and easiest to deal with) may use either narrow-band aperture photometry or imaging. Imaging is a bigger reduction headache, but can also tell you where the action is going on. Reddening is always a potential problem across some regions, if seldom on galaxy-wide scales. One also needs to allow for the contribution of the adjacent [N II] forbidden lines in deriving pure Hα intensities. There are now hundreds of integrated Hα fluxes for galaxies, spanning Hubble types, luminosity, and environment. Here again, it is frequently useful to deal with an equivalent width for the line, giving a normalized SFR compared to its past average. Kennicutt and Kent (1983, AJ 88, 1094) show this relation between Hubble type and EW(Hα) (as usual, courtesy of the AAS):
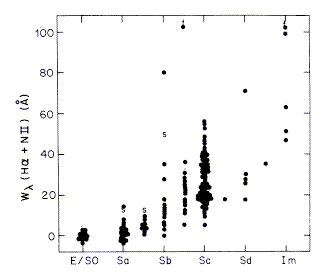
Not surprisingly, the SFR per unit starlight climbs to later Hubble types (toward Sc). To some extent, this reflects the dominant bulges of earlier types, and without information on the gas content it is not so clear what happens within the disk itself.
Models of an evolving population with various SFR histories can also predict broad-band colors as well as EW(Hα); it turns out the Hα is vastly more sensitive to bursts of small relative mass. These figures from Kennicutt in Stellar Populations, and Kennicutt, Tamblyn, and Congdon 1994 (ApJ 435, 22) compare models with various SFR(T) to spiral galaxies; the dispersion and thus discrimination among models is much less for continuum colors. One way to think of this is that the Hα equivalent width is a color index with baseline running all the way from 6563 Å to the Lyman continuum in the far UV.
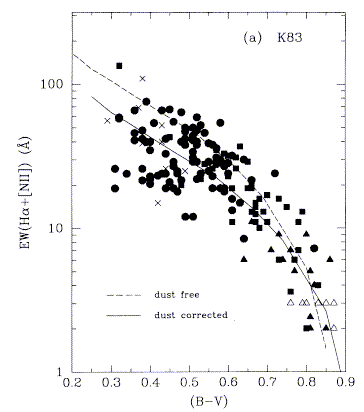
The curves are models with different (declining) star-formation histories. The uppermost systems in their Fig. 2 (above, courtesy AAS) are those in which transient bursts of star formation must be taking place. There will be more to say about starburst systems later.
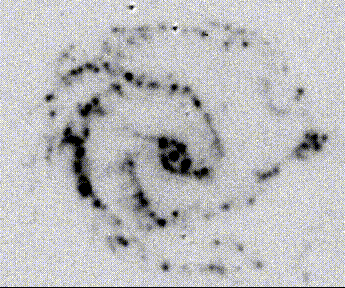 Emission-line images allow mapping of the distribution in both space and
luminosity of large numbers of
individual H II regions (more properly complexes with unresolved or barely
resolved structure). The example at right, NGC 5427, shows numerous H II regions
and clumps of them in a continuum-subtracted
Hα+[N II]
image. The luminous H II regions often align very well with
optical spiral features, but not usually so well that the arms are visible
in the H II regions alone. Rings of star formation are not uncommon. There
is a range of concentration to spiral arms; Hodge (1985 PASP 97, 688)
has quantified
this with a mean vs. variance statistic. The luminosity function of H II
regions is frequently close to a power-law form (Kennicutt et al. 1989, ApJ
337, 761) but there are variations among galaxies such that it is not clear
whether the luminosity distribution or clumping properties change. This
kind of analysis is particularly vulnerable to effects of changing linear
resolution, in making a number of small H II regions look like a single
luminous one. The proper distinction is not obvious. Note that in Soviet
literature, the terminology concentrates on stars and not the gas - giant H
II regions are generally identical with superassociations. Both tend to
clump on somewhat larger scales - complexes - which might be a more robust
way to quantify star-forming regions.
Emission-line images allow mapping of the distribution in both space and
luminosity of large numbers of
individual H II regions (more properly complexes with unresolved or barely
resolved structure). The example at right, NGC 5427, shows numerous H II regions
and clumps of them in a continuum-subtracted
Hα+[N II]
image. The luminous H II regions often align very well with
optical spiral features, but not usually so well that the arms are visible
in the H II regions alone. Rings of star formation are not uncommon. There
is a range of concentration to spiral arms; Hodge (1985 PASP 97, 688)
has quantified
this with a mean vs. variance statistic. The luminosity function of H II
regions is frequently close to a power-law form (Kennicutt et al. 1989, ApJ
337, 761) but there are variations among galaxies such that it is not clear
whether the luminosity distribution or clumping properties change. This
kind of analysis is particularly vulnerable to effects of changing linear
resolution, in making a number of small H II regions look like a single
luminous one. The proper distinction is not obvious. Note that in Soviet
literature, the terminology concentrates on stars and not the gas - giant H
II regions are generally identical with superassociations. Both tend to
clump on somewhat larger scales - complexes - which might be a more robust
way to quantify star-forming regions.
Not all the star-powered Hα emission originates in discrete H II regions. Most spirals have a substantial diffuse interstellar medium which contributes as much as half the integrated line flux (see, for example, Ferguson et al. 1996 AJ 111, 2265). Several studies of its ionization level and energetics suggest that much of its ionization comes from Lyman continuum photons which manage to leak out of individual H II regions. This component to some extent makes up for whether individual regions are matter - or ionization-bounded in estimating a global SFR.
Ultraviolet intensity The mass-lifetime relation for stars tells us that stars that are bright in the UV (beyond the level of the hot evolved stars in ellipticals) must be fairly young, less than 109 years for early A stars. Thus, there has been interest in seeing massive and young stars directly in the UV, where one traces stars not massive or hot enough to produce H II regions. The measurement is analogous to the scaling used for Hα interpretation, except one deals now with luminosity in energy units rather than photon units, and we see the photospheric light directly. However, reddening (extinction) is a strong effect and correspondingly serious uncertainty. At these wavelengths, dust gives a "picket-fence" effect, with very little column density range between no significant extinction and no significant transmission. Comparison between Hα and UV imagery has proven very interesting, with the detailed correspondence being less than exact.
Cowie et al. (1988 ApJL 332, L29, and more detail in two conference papers referenced therein) have noted that the stars responsible for UV light are the same ones that go supernova and produce most of the metals that can be recycled for subsequent star formation, as well as being measurable through line emission. There is this an integral constraint relating (emitted-frame) UV light from galaxies and the rpesent-epoch metallicity of galaxies. Current results (for example from redshift surveys in the Hubble Deep Field) indicate that most of the star formation has happened at z<3 and a nontrivial fraction since z ~ 1. They calculate that the surface brightness (at emitted frequency ν) needed to have produced a density ρZ of metals (in this form it's a volume mass density) is εm (ρZ)c / 4 π where εm = 2840 erg/g Hz for a Salpeter power-law IMF.
Far-Infrared Emission: (Much of this is a reiteration of the dust lecture.) The IRAS survey showed that far-IR emission is ubiquitous among spiral and irregular galaxies, even some for which optical data suggested a very modest dust content. Some fraction of this emission is powered by young stars, making far-IR emission a very tempting indicator of star formation if we can understand it properly. For thermal emission, dust grains are heated by absorption of starlight, which operates most effectively in the blue and UV as the wavelength comes closer to the characteristic grain size. The grains cool by (approximately) black-body emission, modified by a wavelength-dependent emissivity cause largely by the fact that the grains are smaller than the blackbody peak wavelength and thus cannot radiate such wavelengths as efficiently as a perfect radiator. The peak emission typically correspond to a blackbody temperature 20-40 K; a significant range must be present to account for the far-IR spectral shapes. Sometimes several discrete components are fit, including very cool dust measured in the sub-mm window. The components are sometimes attributed to different regimes of heating: environments of OB stars, regions near cooler stars, and so-called infrared cirrus emission from a widely distributed grain population heated only by the average ambient stellar radiation field. Note that the interpretation of mid-IR (10-nicron) emission is complicated by the small grain sizes; such a grain may absorb a single UV photon and be heated well above the equilibrium temperature for the radiation field, thus emitting at a temperature well above that appropriate to its location.
Exact interpretation of the UV-optical-IR energy balance is incredibly messy, requiring knowledge of the exact distribution of various stellar types and grain populations. Global considerations are more interesting. That is, the total energy removed by dust absorption in the visible and UV must emerge in the far-IR. For some galaxies, most of the UV light is absorbed by dust (just how much is a matter of, ahem, heated debate). In this case, the luminosity from 10-300 microns equals that emitted from 912-3000 Å or so. Empirically, there is a tight relation between total far-IR emission and Hα, suggesting that the far-IR emission is strongly coupled to current SFR. This has been used to calibrate relations between FIR luminosity and SFR, but there are important uncertainties - how many ways are there to heat dust grains?
Radio Continuum Emission: Star-forming galaxies and galactic disks are copious emitters of centimeter-wavelength radio emission,much of which must be connected with star formation. This can be seen from morphological considerations in individual galaxies (for example, in Hα vs. radio maps of NGC 1569 and 2276), and the suspiciously tight correlation between far-IR and 6-20 fluxes for galaxies of a wide variety of types. The connection may be rather indirect. The radio spectra of these systems are not the flat, thermal free-free spectra of individual H II regions, but nonthermal such as in synchrotron radiation. Apparently there is a dominant role for particles accelerated perhaps in supernova remnants, radiating while spiralling through large-scale magnetic fields. In this case, the radio emission traces star formation through the supernova rate.
Radio emission is a valuable tracer in heavily obscured regions, such as IRAS-selected galaxies. In fact, radio mapping proves to be a useful tool in identifying IR-loud galaxies at faint optical magnitudes, since VLA positions are much more accurate than IRAS centroids.
CO Molecular-Line Studies: The discovery that much of a galaxy's interstellar medium resides in massive clouds (106-107 solar masses, giant molecular clouds or GMCs) revolutionized our view of star formation. These clouds are the immediate precursors of star formation, the "placental clouds" of giant H II regions. Most optically visible H II regions in fact exist as blisters blown on the edges of such clouds. If one assumes that cloud clumps are everwhere similar, and that any threshold mass for forming star clusters is also constant, the CO intensity will indirectly tell us the SFR. Existing correlations in fact are consistent with this notion for normal galaxies.
This notion will clearly break down under extreme conditions, and in fact starburst systems have much of their molecular gas in compact high-density configurations. Also, at low metallicity, the amount of CO per H2 mass will change, largely because C and O abundances are lower.
Integrated Starlight - Time-integrated Constraints: The total luminosity of a galaxy at some given wavelength gives us an important clue to the star-forming history. It is the sum of the luminosities of all stars that have not reached their final compact states. Blue light is emitted most efficiently by stars of a few solar masses; if their formation has continued so that such stars (not older giants or main-sequence stars) dominates the optical light, their formation rate is given by Gallagher, Hunter, and Tutukov (1984, ApJ 284, 544) as SFR (solar masses/yr)= 2.9 x 10-9 LB/LSun.
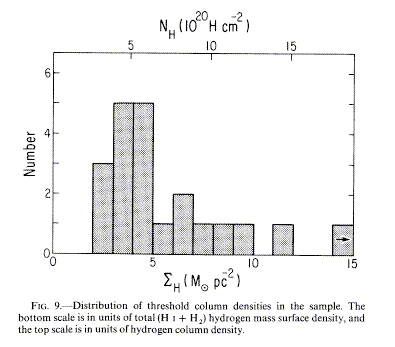
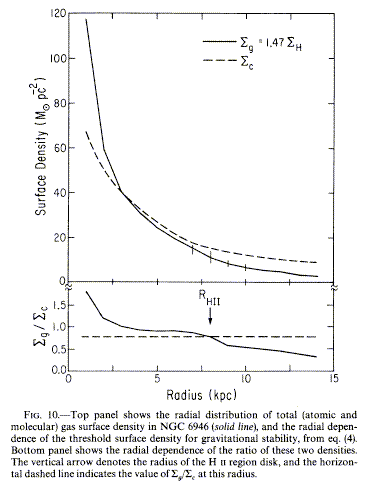
The Star-Formation Law in Galactic Disks: Since stars come from gas, and we can now measure more or less directly the appropriate gas components, it is useful to ask how SFR depends on local gas properties. A favorite, simple contender for many years has been the Schmidt law: SFR = constant x σgas N where N is the significant parameter. Fits to this law have given contradictory results. The problem has been accounted for by the realization that there is a threshold surface density of gas below which essentially no star formation takes place. If the Schmidt law applies, it is far above this threshold. There is a plausible dynamical explanation (Kennicutt 1989 ApJ 344,685; Zasov and Simikov 1988 Astrofizika 29, 190) involving stability of disk gas in the presence of rotational shear; gas doesn't collapse unless it is dense enough to be unstable under the local shear conditions (Quirk 1972 ApJL 176, L9; Toomre 1964 ApJ 139, 1217). The dependence of SFR on surface density and the relation of the extent of the star-forming zone to the stability criterion are shown in Figs. 9 and 10 of Kennicutt 1989:
Last changes: 9/2009 © 2000-9