The most useful description of cosmological models involves general relativity. Its geometric basis allows a natural treatment of light propagation along geodisics, which is how we get most of our information. Static solutions to Einstein's equations are unstable unless there is some repulsive force giving rise to nonzero cosmological constant Λ. A description of this kind has two locally observable parameters, in terms of the behavior of a scale factor R. This is defined so that the evolution of the distance between two comoving points (that is with no peculiar velocities superimposed on those from the cosmological expansion) evolves as r12 = r0 R(t). These parameters are the Hubble ratio (not quite constant since it will in general change with cosmic time)
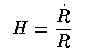
and the density or deceleration parameter
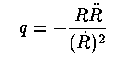
For both of these, a subscript 0 indicates their evaluation at the present epoch. q is related to the open or closed nature of the universe. The critical closure density is ρ0 = 3 H² / 8 ρG as may be easily derived from Newtonian physics. Consider a volume element of gas in a uniform medium of density ρ at distance r from some arbitrary central point. Using a theorem of Newton, the gravitational attraction of a uniform medium outside r has no net effect, so the gravitational force due to the material within r generates a potential - GM(< r)ρ dV/r = -4G ρ r² ρ² dV/3 for the matter in the volume element dV. Its kinetic energy for a Hubble-like flow is mv²/2 or ρ dV H² r² /2. At critical density, the net energy is zero or alternately the material in dV is marginally bound: 4 G π r² ρ>² dV /3 = ρ dV H² r² /2 This is satisfied for the value of ρ0 given above. The density in units of ρ0 is often denoted by Ω. For Λ=0, q = Ω/2 so that q0 = 1/2 is the critical value.
Enormous effort has gone into the determination of H0 and q0 via "classical" tests using galaxies as standard candles. Measurement of H0 has been discussed in the distance-scale lecture. The problem with measuring the deceleration parameter is that the universe is close to the critical density, so that departures from this critical value become apparent only over such large path lengths that galaxy evolution becomes the dominant factor. What little we know about galaxy evolution says that galaxies won't be standard candles. These tests are well documented in the review by Sandage 1988 (ARA&A 26, 561) in an eloquent testimonial to the ultimate failure of most of them. These rely on the propagation of radiation in an expanding metric and the consequent breakdown of the inverse-square law for intensities and the inverse angular diameter-distance relation (more later on what distance means in this context). Further discussion of these tests may be found in Weinberg, Gravitation and Cosmology, Peebles, Physical Cosmology, and ch. 3 of Weedman, Quasar Astronomy.
Hubble diagram or magnitude-redshift test. Assume we have a set of galaxies with unchanging and known intrinsic brightness. It has been popular to take radio galaxies or third-brightest cluster members for this; radio galaxies in the K-band are especially well-behaved. At small redshifts, the Hubble expansion makes the magnitude-log z relation linear, with some scatter due to galaxy properties and our ignorance of just how to select a perfectly uniform set of galaxies. At high z, the relation may curve for various q0. To see how, consider various measures of distance to an object of redshift z. The proper distance is that traversed by a photon in its own frame from there and then to here and now, which is to say DP = 1/c × light travel time. The luminosity distance is that which makes the inverse-square law work as it does in a flat universe: luminosity/flux = 4 π DL². Finally, the angular diameter distance is that for which the linear size-angular size relation has its familiar small-angle form θ = length/DA.
For the standard (Friedman) model,
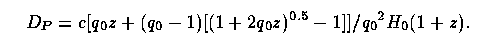
This is one of a set of closed forms worked out by Mattig (1958 Astron. Nachr. 284, 109) in a demonstration of analytical virtuosity starting from the Robertson-Walker metric and curvature scale in a Friedmann model. [I tried to reproduce this derivation as an inquisitive grad student, and gave up after two days when it wasn't getting any closer. George Blumenthal said it took him three days.] Then we have DL = (1+z) DP and DA = DL/(1+z)² which simplify in various ways for the special cases q0=0,1/2,1. For example, if q0=1, the lookback time τLB = DP/c = (H0)-1(z/{1+z}).
In principle, the curvature in the extended Hubble diagram for standard candles can give q0 as shown by Weinberg p. 448 quoting Sandage. Big news has been the finding that high-redshift type Ia supernovae show evidence of upward curvature in the analogous magnitude-redshift relation, implying a nonzero cosmological constant. Type Ia objects are] useful because they have a narrow absolute-magnitude dispersion to begin with, and much of this dispersion is corralated with independently measurable fading timescale, plus the fact that they should all have the same kind of progenitor which formed its own heavy elements so that initial-metallicity effects should be small. The evidence is shown in Fig. 4 of Riess et al. (1998 AJ 116, 1009, reproduced by permission of the AAS):
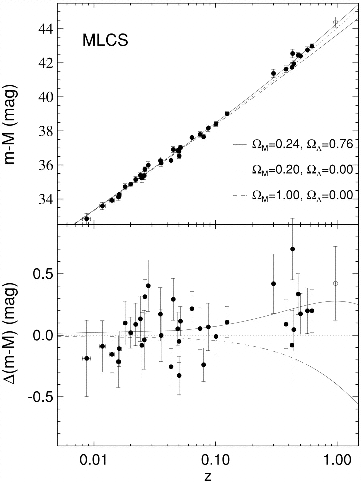
The differences among various values of q0 become important only for z > 1. Applying this test to real data on galaxies is further complicated by various effects, some of whioch don't enter for the supernova test. The K-correction accounts for the fact that one is no longer observing the same part of the spectrum at various redshifts, and for the decrease in photon arrival rate (by a factor 1+z) even if one follows the same emitted-frame wavelength with z. Galaxy evolution, both stellar and dynamical, turns out to be so strong that it's much easier to measure than q0. For cluster galaxies, richness effects enter - at high redshift it's easier to pick out rich clusters whose nth brightest members are then brighter than expected. It is not clear that this is the path to q0 because of the dominant role of galaxy luminosity and spectral evolution.
The angular diameter - redshift test looks for a breakdown of the inversion relation between distance and angular diameter of some set of standard measuring rods (say galaxy isophotes or radio-galaxy lobe separations). Surface brightnesses must be corrected for dimming by (1+z)4 due to expansion of space plus photon energy and arrival-time decreases. The form of this has been used as a test (the Tolman test) that redshifts really correspond to an expansion, and not to once-popular "tired-light" phenomena (Sandage and Perelmuter 1990 ApJ 350, 481; 361, 1; 1991 ApJ 370, 455, Wirth 1997 PASP 109, 344). Here again, one might have to deal with evolutionary effects in such objects as radio sources - have they always been the same size? At least with galaxy structures one has some control over how much dynamical evolution might have gone on.
It is interesting that, for any given positive value of q0, there exists a minimum in the θ(z) relation for any linear size; things at higher redshift look bigger again because they were quite nearby when the light was emitted. For q0=1/2, the angular diameter goes through a minimum at z=5/4. Using the analytical form listed, for example, in Lang, Astrophys. Formulae, eqn. 5-314, we have:
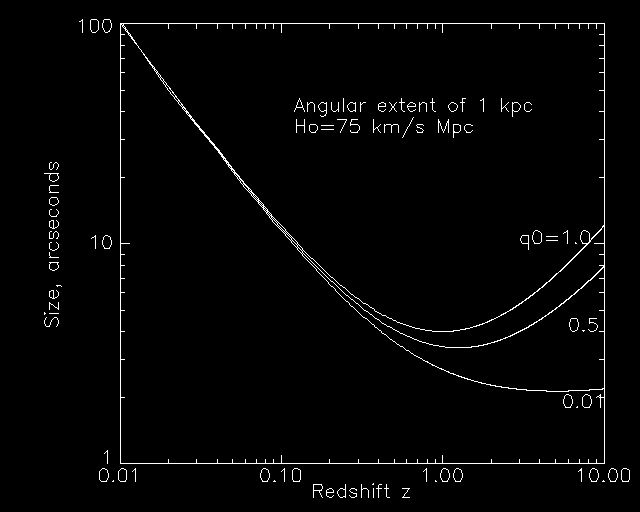
(If you want to experiment with this, here's some simple IDL code which generated the plot). This effect may be in part responsible for the large apparent sizes of very-high-redshift radio galaxies (see Djorgovski in Nearly Normal Galaxies, for example). In interpreting sizes of high-redshift objects, though, surface-brightness dimming can be a dominant effect.
Galaxy number counts may be used to trace the history of the volume per galaxy, so that the N(z) relation implies R(t) since the scale factor R scales as (1+z)-1. If we could count a conserved population over a wide redshift range, we could learn q0 directly from its definition. An early attempt used six-color mapping to estimate photometric redshifts (Loh and Spillar 1986 ApJLett 307, L1). Modelling with a standard luminosity function, they get Ω= 0.9 +0.7-0.5 from 1000 "field" galaxies. This is independent of color evolution, but is dependent on luminosity evolution and merging; both these processes could change the number of galaxies in a given luminosity range with redshift. As discussed by Sandage 1988, most applications of this test are more sensitive to galaxy evolution than to cosmology (because the universe is old enough for us to be here talking about it).
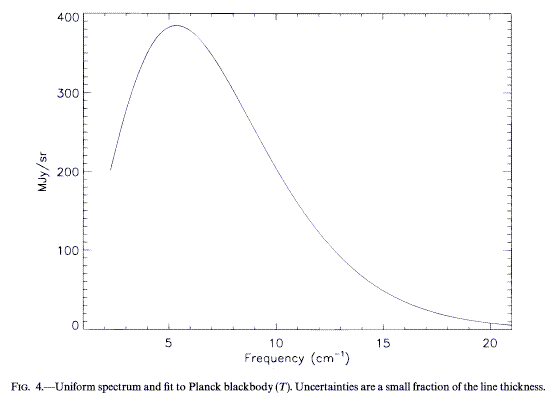
There are additional constraints from local (or indeed laboratory) observations. Most prominent is the cosmic microwave background. This is the radiation field at the epoch of (re)combination, when the universe first became transparent enough for radiation to propagat freely over cosmologically interesting distances. At the high densities then, the radiation field was fully themalized (blackbody). Since then the observed temperature has dropped due to redshifting (a redshifted blackbody is another lower-temperature blackbody). See Peebles, chapter 7, for some complications. Recombination was somewhere around z ~ 104 set by the temperature at which hydrogen ionizes and the observed CMB temperature (which we know from COBE to be 2.785 K, Mather et al 1990 APJLett 354, L37 and Smoot et al 1991 ApJLett 371, L1). The CMB is highly isotropic (except for a dipole term thought to reflect our motion with respect to the large-scale velocity defined by the CMB emission surface) and embarrassingly smooth. Its spectrum is as perfect a blackbody as can be measured: from Fig. 4 of Fixsen et al. 1996 (ApJ 473, 576, by permission of the AAS),
We would expect some lumps corresponding to protogalaxies and -clusters, since it is hard enough to understand how galaxies form by z ~ 5 from inhomogeneities at recombination. These were finally detected in a convincing way by the COBE group, with subsequent confirmation by ground-based observations from Tenerife and Antarctica as well as balloon-borne instruments. The fluctuations, as measured at a resolution of a few degrees, are at the level Δ T / ~ 3 × 10-6, which is (to factors "of order unity") the density contrast Δ ρ / ρ of fluctuations. Linear development of perturbations won't cut it to clump matter fast enough; there is something major here that we don't know about making galaxies. I am holding out for nonbaryonic matter already clumped at recombination and providing seeds for forming baryonic structures, but then I could be convinced otherwise if anything resembling evidence shows up. The CMB was one of the major downfalls of a steady-state picture; something has clearly changed since the time when space was uniformly filled with 4000-K plasma.
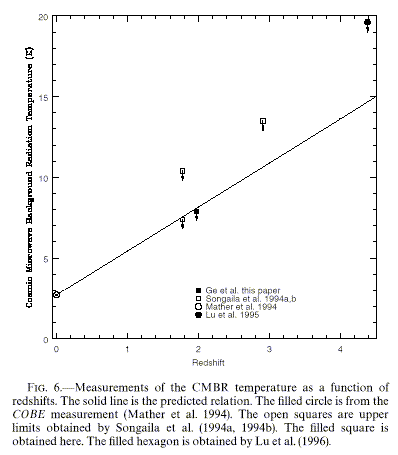
Absorption of the CMB by hot gas in cluster is expected (the Sunyaev-Zeldovich effect) and has been observed after years of upper limits - this is interesting as direct confirmation that we are not seeing some unknown local effect, since the CMB comes from behind clusters at substantial redshift. Note that the CMB temperature should scale as 1+z; measurements of low-energy fine-structure levels (specifically C II*) in QSO absorption-line systems indeed show this effect. As shown by Ge, Bechtold, and Black 1997 ApJ 474, 67, (courtesy of the AAS),
In retrospect, the first hint of the CMB was the excitation temperature of interstellar CN seen in absorption at 3874 Å against galactic stars, with observations tracing back to Adams 1941 (ApJ 93, 11; see Thaddeus 1972 ARA&A 10, 305 for a fuller history). As discussed by Roth, Meyer, and Hawkins (1993 ApJL 413, L67), these lines are excited by absorbing radiation at 1.3 and 2.6mm. These observations have some philosophical interest in showing the uniformity of this radiation on galactic scales.
Last changes: 11/2009 © 2000-9